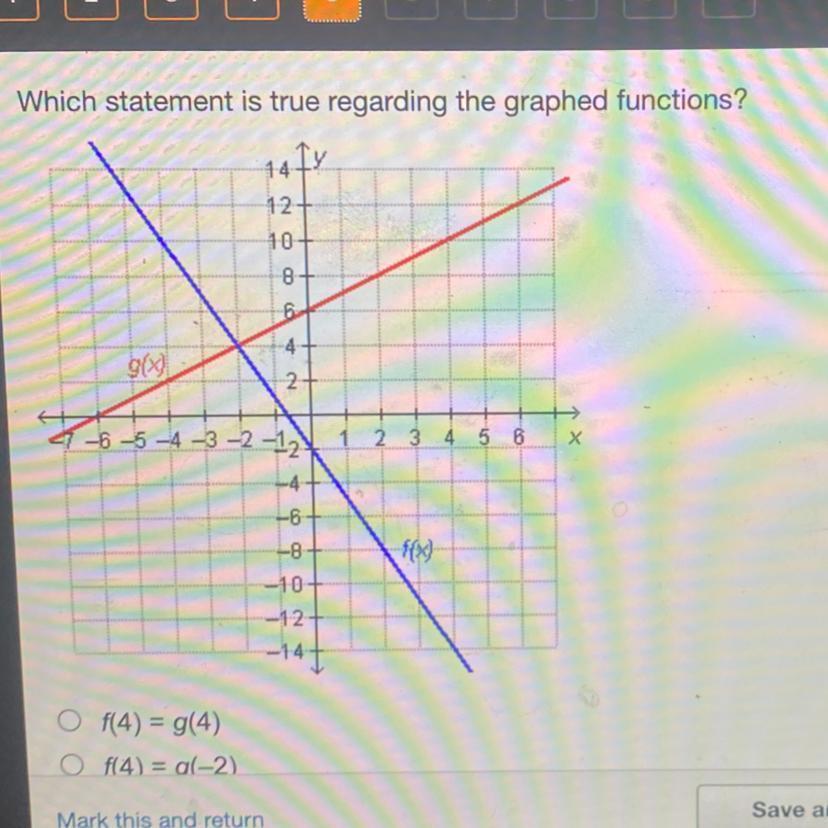
Which statement is true regarding the graphed functions?
141x
12-
10-
g(x)
8-
3)
6
fin
2+
7-6-5-4-3-2-12 1 2 3 4 5 6
-4
-6
-8+
ܘ
-10+
-12+
-14
f(x)
个x
X

a. The addition to retained earnings is $370,120,000.

b. The dividend yield was 69.52%.

a. The amount paid out as dividends can be calculated as:

Dividends = Earnings x Dividend payout ratio

Dividends = $487,000,000 x 0.24

Dividends = $116,880,000

Therefore, the addition to retained earnings would be:

Addition to retained earnings = Earnings - Dividends

Addition to retained earnings = $487,000,000 - $116,880,000

Addition to retained earnings = $370,120,000

b. Dividends per share can be calculated by dividing the total dividends paid by the number of outstanding shares:

Dividends per share = Dividends / Number of shares

Dividends per share = $116,880,000 / 100,000,000

Dividends per share = $1.1688 per share

The dividend yield can then be calculated as:

Dividend yield = Dividends per share / Stock price x 100%

Dividend yield = $1.1688 / $168 x 100%

Dividend yield = 0.6952 x 100%

Dividend yield = 69.52%

for such more question on dividend yield

https://brainly.com/question/13402434

#SPJ11

a. The addition to retained earnings is: $370,120,000.

b. The dividend yield is: 69.52%.

a. The amount that was paid out in form of dividends is gotten from the expression:

Dividends = Earnings × Dividend payout ratio

We are given:

Earnings = $487,000,000

Dividend payout ratio = 0.24

Thus:

Dividends = $487,000,000 × 0.24

Dividends = $116,880,000

The additional retained earnings is expressed in the form of:

Additional retained earnings = Earnings - Dividends

Thus:

Additional retained earnings = $487,000,000 - $116,880,000

Additional retained earnings = $370,120,000

b. Dividends per share gotten from the expression:

Dividends per share = Dividends ÷ Number of shares

We are given the parameters as:

Dividends = $116,880,000

Number of shares = 100,000,000

Thus:

Dividends per share = $116,880,000 ÷ 100,000,000

Dividends per share = $1.1688 per share

The dividend yield is gotten from the expression:

Dividend yield = (Dividends per share ÷ Stock price) * 100%

We are given the parameters as:

Dividends per share = $1.1688

Stock Price = $168

Thus:

Dividend yield = ($1.1688 ÷ $168) * 100%

Dividend yield = 0.6952 × 100%

Dividend yield = 69.52%

Read more about dividend yield at: https://brainly.com/question/20704820

#SPJ4

Q1.  Farmer Joe will need approximately 15.71 feet of fence to enclose the rose bush with 1 foot of clearance.

Q2.  the area of the rose bush bed is approximately 7.07 square feet, and the fertilizer bag covers 35 square feet, Farmer Joe will have more than enough fertilizer for the rose bush.

Q1: To calculate the amount of fence Farmer Joe will need for the rose bush, we need to consider the perimeter of the circular fence.

The diameter of the rose bush is 3 feet, so the radius (half of the diameter) is 3/2 = 1.5 feet. Since he needs 1 foot of clearance around the bush, the radius of the circular fence will be 1.5 + 1 = 2.5 feet.

The formula for the circumference (perimeter) of a circle is C = 2πr, where π is a mathematical constant approximately equal to 3.14159. Plugging in the value of the radius, we get:

C = 2 * 3.14159 * 2.5 = 15.70795 feet.

Therefore, Farmer Joe will need approximately 15.71 feet of fence to enclose the rose bush with 1 foot of clearance.

Q2: The fertilizer bag covers an area of 35 square feet. To determine if it will be enough for the rose bush, we need to calculate the area of the circular bed where the rose bush will be planted.

The area of a circle is given by the formula A = πr^2. Plugging in the value of the radius (1.5 feet), we have:

A = 3.14159 * (1.5)^2 = 3.14159 * 2.25 = 7.06858 square feet.

Since the area of the rose bush bed is approximately 7.07 square feet, and the fertilizer bag covers 35 square feet, Farmer Joe will have more than enough fertilizer for the rose bush.

For more such questions on area visit:

https://brainly.com/question/25292087

#SPJ8

All angles lying between 0 and 2π satisfying the condition cos x = 1/2 are π/3 and 5π/3. These angles are mainly: π/3, 5π/3 + 2π, and 5π/3 + 4π, and can be simplified to: π/3, 11π/3, and 19π/3.

Given the condition cos x = 1/2, we know that the angle x must be one of the angles for which cos is equal to 1/2, which are π/3 and 5π/3. However, the range of x is 0 ≤ x ≤ 2π. Therefore, we must find all the angles in this range that satisfy the given condition. These angles are: π/3, 5π/3 + 2π, and 5π/3 + 4π, which simplifies to: π/3, 11π/3, 19π/3.

Since 11π/3 and 19π/3 are greater than 2π, we need to subtract 2π from each to get them into the range 0 ≤ x ≤ 2π, which gives: π/3 and 5π/3 as the solutions in this range.

Therefore, all angles between 0 and 2π satisfying the condition, cos x= 1/2 are:π/3 and 5π/3.

We know that cos x is periodic, with a period of 2π, and that its value is equal to 1/2 at two different angles in the interval [0, 2π), which are π/3 and 5π/3. Since we are asked to find all angles that satisfy the condition cos x = 1/2 in this interval, we must add 2π to the second solution, which gives us 11π/3.

However, this is greater than 2π, so we must subtract 2π to get it into the desired range, which gives us 5π/3. Similarly, we must add 4π to the second solution, which gives us 19π/3. However, this is also greater than 2π, so we must subtract 2π to get it into the desired range, which gives us 11π/3.

Therefore, the solutions in the interval [0, 2π) are π/3 and 5π/3. These are the only solutions in this interval since the cosine function has a maximum value of 1 and a minimum value of -1, so it can only equal 1/2 at two angles between 0 and 2π. Thus, all angles between 0 and 2π satisfying the condition cos x = 1/2 are π/3 and 5π/3.

To know more about the cosine function, visit:

brainly.com/question/3876065

#SPJ11

The equations of the tangents to the curve are y = 3x - 6 and y = -3x + 30.

To find the equations of the tangents to the curve, we need to determine the slope of the tangent line at the given point of tangency.

The given curve is defined by the parametric equations x = 6t^2 - 2 and y = 4t^3 - 2.

We can eliminate the parameter t by expressing t in terms of x.

Rearranging the first equation, we have t^2 = (x + 2) / 6, and taking the square root of both sides, we get t = ±√((x + 2) / 6).

Substituting this value of t into the equation for y, we have y = 4(±√((x + 2) / 6))^3 - 2.

Simplifying this expression, we obtain y = ±(4/3)√((x + 2)^3 / 6) - 2.

Now, let's find the slopes of the tangents at the point (8, 6). We take the derivative of y with respect to x and evaluate it at x = 8.

Differentiating y with respect to x, we get dy/dx = ±(4/3)√(2(x + 2)^3 / 3)(1 / 2) = ±(2/3)√((x + 2)^3 / 3).

Evaluating the derivative at x = 8, we have dy/dx = ±(2/3)√((8 + 2)^3 / 3) = ±(2/3)√(10^3 / 3) = ±(2/3)√(1000/3) = ±20√10/3.

Since the slopes of the tangents are given by the derivative, the two possible slopes are ±20√10/3.

Now we can find the equations of the tangents using the point-slope form. Using the point (8, 6), we have:

y - 6 = (±20√10/3)(x - 8).

Simplifying these equations, we get:

y = 3x - 6 and y = -3x + 30.

Therefore, the equations of the tangents to the curve that pass through the point (8, 6) are y = 3x - 6 (the smaller slope) and y = -3x + 30 (the larger slope).

To learn more about tangents, click here: brainly.com/question/31186629

#SPJ11

Our power series is F(x) = ∑(n=0 to ∞) of (-1)ⁿ × x⁶ⁿ.The interval of convergence for the power series representation of F(x) is -1 < x < 1.

To find the power series representation for the function F(x) = 1/(1 + x⁶), we can use the geometric series formula.

The geometric series formula states that for |r| < 1, the series ∑(n=0 to ∞) of rⁿ converges to 1/(1 - r).

In this case, we can rewrite F(x) as:

F(x) = 1/(1 + x⁶) = (1 - (-x⁶))⁻¹

Now, we can see that this is a geometric series with r = -x⁶. Using the geometric series formula, we can express F(x) as a power series:

F(x) = (1 - (-x⁶)⁻¹) = ∑(n=0 to ∞) of (-x⁶)ⁿ

Expanding this series, we get:

F(x) = ∑(n=0 to ∞) of (-1)ⁿ × x⁶ⁿ)

So, the power series representation for F(x) is:

F(x) = ∑(n=0 to ∞) of (-1ⁿ) × x⁶ⁿ

To determine the interval of convergence for this power series, we need to find the values of x for which the series converges.

The interval of convergence is determined by the radius of convergence, which can be found using the ratio test. The ratio test states that for a power series ∑(n=0 to ∞) of a_n × (x - c)ⁿ, the series converges if the limit of |a_(n+1) / a_n| as n approaches infinity is less than 1.

In this case, our power series is:

F(x) = ∑(n=0 to ∞) of (-1)ⁿ × x⁶ⁿ

Using the ratio test, we have:

|((-1)ⁿ⁺¹ × x⁶[tex]^([/tex]ⁿ⁺¹[tex]^)[/tex]) / ((-1)ⁿ × x⁶ⁿ)| = |(-1) × x⁶| = |x⁶|

The limit of |x⁶| as n approaches infinity is |x⁶|. For the series to converge, |x⁶| must be less than 1. Therefore, the interval of convergence is:

|x⁶| < 1

which implies:

-1 < x⁶ < 1

Taking the sixth root of each inequality, we have:

-1 < x < 1

So, the interval of convergence for the power series representation of F(x) is -1 < x < 1.

Learn more about series

brainly.com/question/12474324

#SPJ11

The area of a regular n-gon with side length s is given by ns2(2 + √3)/4, or ns2tan(π/n)/4 using the trigonometric identity.

Consider a regular n-gon with side length s. We can divide the n-gon into n congruent isosceles triangles, each with base s and equal angles. Let one such triangle be denoted by ABC, where A and B are vertices of the n-gon and C is the midpoint of a side.

The angle at vertex A is equal to 360°/n since the n-gon is regular. The angle at vertex C is equal to half of that angle, or 180°/n, since C is the midpoint of a side. Thus, the angle at vertex B is equal to (360°/n - 180°/n) = 2π/n radians.

We can now use trigonometry to find the area of the triangle ABC: the height of the triangle is given by h = (s/2)tan(π/n), and the area is A = (1/2)sh. Since there are n such triangles in the n-gon, the total area is given by ns2tan(π/n)/4.

Using the fact that tan(π/12) = √6 - √2, we can simplify this expression to ns2(√6 - √2)/4. Multiplying top and bottom by (√6 + √2), we obtain ns2(2 + √3)/4.

For such more questions on Trigonometric identity:

https://brainly.com/question/24496175

#SPJ11

The production level that minimizes the average cost per unit is 0.64 units.

To find the production level that minimizes the average cost per unit, we need to first find the average cost function.
The average cost function is given by:
AC(x) = c(x)/x

Substituting c(x) = 5x - 8√x - 2, we get:
AC(x) = (5x - 8√x - 2)/x

To minimize the average cost per unit, we need to find the value of x that minimizes the average cost function.
To do this, we need to take the derivative of the average cost function with respect to x and set it equal to 0:
d/dx AC(x) = (5 - 4/√x)/x^2 = 0

Solving for x, we get:
5 = 4/√x
√x = 4/5
x = (4/5)^2
x = 0.64

Therefore, the production level that minimizes the average cost per unit is 0.64 units.

Know more about the average cost here:

https://brainly.com/question/29509552

#SPJ11

The probability that the Watson family eats dinner together at least six times during a 7-day period can be calculated using the binomial distribution. The probability is approximately 0.0332 or 3.32%.

Let's define success as the event that the Watson family eats dinner together on a particular day, with a probability of success being 2/5. Since the events of eating dinner together on different days are independent, we can use the binomial distribution to calculate the probability.  

To find the probability of having at least six successful events (eating dinner together) in a 7-day period, we need to sum the probabilities of having exactly 6, 7 successful events, and so on, up to 7.

Using the binomial probability formula, P(X=k) = C(n, k) * p^k * (1-p)^(n-k), where n is the number of trials (7 in this case), k is the number of successful events (6 or 7), and p is the probability of success (2/5), we can calculate the probabilities for each k and sum them.

P(X≥6) = P(X=6) + P(X=7) ≈ 0.0332 or 3.32%

Therefore, there is approximately a 3.32% chance that the Watson family will eat dinner together at least six times during any 7-day period.

Learn more about distribution here:

https://brainly.com/question/29664127

#SPJ11

Under the given conditions, the expression tan(θ) evaluates to -3/4.

To evaluate the expression tan(θ) given the conditions cos(θ) = -1/3 in quadrant III and sin(θ) = 1/4 in quadrant II, follow these steps:

Recall the definition of tangent in terms of sine and cosine:
tan(θ) = sin(θ) / cos(θ)

Use the given conditions for sine and cosine:
sin(θ) = 1/4 (in quadrant II)
cos(θ) = -1/3 (in quadrant III)

Substitute the given values into the tangent formula:
tan(θ) = (1/4) / (-1/3)

Simplify the expression by multiplying the numerator and the denominator by the reciprocal of the denominator:
tan(θ) = (1/4) * (-3/1)

Multiply the numerators and the denominators:
tan(θ) = (-3) / 4

So, the expression tan(θ) evaluates to -3/4 under the given conditions.

To learn more about the tangent function visit : https://brainly.com/question/1533811

#SPJ11

To evaluate the series Σ(3^n/(141·3²ⁿ) from n=1 to infinity converges or diverges, we can use the ratio test.

The ratio test states that if the limit of the absolute value of the ratio of consecutive terms is less than 1, then the series converges absolutely;

if the limit is greater than 1, then the series diverges; and if the limit is exactly 1, then the test is inconclusive.

Let's first apply the ratio test to this series:

| (3ⁿ+¹/(141·3²ⁿ+¹) * (141·3²ⁿ))/(3ⁿ |

= | 3/141 |

= 1/47

Since the limit of the absolute value of the ratio of consecutive terms is less than 1, the series converges absolutely.

To compute the sum of the series, we can use the formula for the sum of a geometric series:

Σ(3ⁿ/(141·3²ⁿ) = 3/141 Σ(1/9)ⁿ from n=1 to infinity

= (3/141) · (1/(1-(1/9)))

= 27/470

Therefore, the series converges absolutely and its sum is 27/470.

Learn more about series : https://brainly.com/question/15415793

#SPJ11

 A Markov chain is a stochastic process that exhibits the Markov property, meaning the future state depends only on the present state, not on the past.

In this case, the given Markov chain can be represented by the transition matrix: | 0 1 0 | | 0 0 1 | | 0 0 1 |

The starting vector is [1, 0, 0].

To find the behavior of the Markov chain, we multiply the starting vector by the transition matrix repeatedly to see how the state evolves.

After one step, we have: [0, 1, 0]. After two steps, we have: [0, 0, 1].

From this point on, the chain remains in state [0, 0, 1] since the third row of the matrix has a 1 in the third column.

This indicates that [0, 0, 1] is a stable vector, as the chain converges to this state and remains there regardless of the number of additional steps taken.

Learn more about markov chain at

https://brainly.com/question/30465344

#SPJ11

x = (0,0)T and x = (0,1)T are both candidates for local minimizers. To determine which (if any) is a local minimizer, we need to perform further analysis, such as computing the Hessian matrix and checking for positive definiteness.

To solve the given optimization problem, we first need to find the gradient of the objective function:

∇f(x) = [∂f/∂X1, ∂f/∂X2]T = [4, 4]T

Now, let's examine each point and find the feasible directions:

At x = (0,0)T:

The constraint X1 + X2 < 2 becomes 0 + 0 < 2, which is true. Also, X1, X2 > 0 is true. Therefore, the feasible directions are any non-negative direction.

At x = (0,1)T:

The constraint X1 + X2 < 2 becomes 0 + 1 < 2, which is true. Also, X1, X2 > 0 is true. Therefore, the feasible directions are any non-negative direction.

At x = (1,1)T:

The constraint X1 + X2 < 2 becomes 1 + 1 < 2, which is true. Also, X1, X2 > 0 is true. Therefore, the feasible directions are any direction in the first quadrant.

At x = (0,2)T:

The constraint X1 + X2 < 2 becomes 0 + 2 < 2, which is false. Therefore, there are no feasible directions at this point.

Next, we need to determine whether there exist feasible descent directions at each point. A feasible descent direction at a point x is a direction d such that f(x + td) < f(x) for some small positive value of t.

At x = (0,0)T and x = (0,1)T:

Since any non-negative direction is a feasible direction at these points, we can simply check if the gradient is non-positive in any non-negative direction. We have:

∇f(x) · d = [4, 4]T · [d1, d2]T = 4d1 + 4d2

Therefore, the gradient is non-positive in any direction with d1 + d2 = 1. These are the directions that lie along the line y = -x + 1 in the first quadrant. Therefore, there exist feasible descent directions at these points.

At x = (1,1)T:We need to check if the gradient is non-positive in any direction in the first quadrant. Since the gradient is positive in all directions, there are no feasible descent directions at this point.

Learn more about Hessian matrix here

https://brainly.com/question/31379954

#SPJ11

Answer:

22,281.73

Step-by-step explanation:

1 kilometer = 1000 Meters

Subtract the 100 meters you already have from 1000.

Multiply 900 times 24.73

Add 22,257 to 24.73

= 22,281.73

This means that Jasmine can plant any number of lily bulbs (y = 0) and allocate the remaining bulbs to tulips (x = 40 or less) to satisfy the given conditions.

To determine the minimum number of tulip bulbs Jasmine could plant while having more tulips than lilies, we need to consider the given conditions.

Let's assume Jasmine plants x tulip bulbs and y lily bulbs.

Based on the conditions given:

Jasmine is planting a maximum of 40 bulbs in total: x + y ≤ 40

She wants more tulips than lilies: x > y

To find the minimum number of tulip bulbs, we want to minimize the value of x.

Considering the condition x > y, we can start by setting y = 0 (minimum number of lily bulbs) and check the feasibility of the other condition.

If y = 0, then x + 0 ≤ 40, which simplifies to x ≤ 40.

So, the minimum number of tulip bulbs Jasmine could plant is 0, as long as the total number of bulbs (x + y) is less than or equal to 40.

This means that Jasmine can plant any number of lily bulbs (y = 0) and allocate the remaining bulbs to tulips (x = 40 or less) to satisfy the given conditions.

Learn more about number here:

https://brainly.com/question/3589540

#SPJ11

The exponential likelihood that the next call would occur in more than 21 seconds but less than 26 seconds is 0.1504, which corresponds to option (C) on the multiple-choice list.

We may use an exponential distribution with a mean of 31 seconds to simulate the period between calls.

The exponential distribution's probability density function is given by:

f(x) = λe^(-λx)

where λ is the rate parameter, which is equal to 1/mean in this case.

So, we have λ = 1/31 and we need to find the probability that the time between calls is between 21 and 26 seconds. This can be expressed as:

P(21 < X < 26) = ∫21²⁶ λe^(-λx) dx

Using a calculator or integration software, we can find:

P(21 < X < 26) = 0.1504

To learn more about the probability distribution function;

brainly.com/question/15353924

#SPJ1

The set S is linearly dependent.

To determine if the set S is linearly independent or dependent, we need to see if any of the vectors in the set can be written as a linear combination of the others.

Let's set up the equation:

a(3/2, 3/4, 5/2) + b(4, 7/2, 3) + c(?, -3/2, 2, 6) = (0,0,0)

To solve for a, b, and c, we can create a system of equations using each component:

3a/2 + 4b + c? = 0
3a/4 + 7b/2 - 3c/2 = 0
5a/2 + 3b + 2c = 0
6c = 0

The last equation tells us that c must be 0, since we can't have a non-zero scalar multiplying the zero vector.

Using the first three equations, we can solve for a and b:

a = (-8/3)c?
b = (5/3)c?

Since c can be any non-zero number, we can see that there are infinitely many solutions to this equation, meaning that the set S is linearly dependent.

Therefore, the answer is option B linearly dependent.

To know more about linearly dependent. refer here:

https://brainly.com/question/31326686

#SPJ11

The poisson probability distribution is used with a continuous random variab .In a Poisson process, where events occur at a constant rate, the exponential distribution represents the time between them.

In reality, the Poisson likelihood dispersion is regularly utilized with a discrete irregular variable, not a nonstop arbitrary variable. The number of events that take place within a predetermined amount of time or space is modeled by the Poisson distribution. Examples of such events include the number of customers who enter a store, the number of phone calls that are made within an hour, and the number of problems on a production line.

The events are assumed to occur independently and at a constant rate by the Poisson distribution. It is defined by a single parameter, lambda (), which indicates the average number of events that take place over the specified interval. The probability of observing a particular number of events within that interval is determined by the Poisson distribution's probability mass function (PMF).

The Poisson distribution's PMF is defined as

P(X = k) = (e + k) / k!

Where:

The number of events is represented by the random variable X.

The number of events for which we want to determine the probability is called k.

The natural logarithm's base is e (approximately 2.71828).

is the typical number of events that take place during the interval.

While discrete random variables are the focus of the Poisson distribution, continuous distributions like the exponential distribution are related to the Poisson distribution and are frequently used in conjunction with it. In a Poisson process, where events occur at a constant rate, the exponential distribution represents the time between them.

To know more about  Poisson distribution refer to

https://brainly.com/question/30388228

#SPJ11

[tex] \sqrt{36 - 25} = \sqrt{11} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ [/tex]

Using the Runge-Kutta method of second order, the approximate value of y when x = 0.02 is is 1.0203045100525125.

To apply the Runge-Kutta method of second order to approximate the value of y when x = 0.02, we can follow these steps:

[tex]y' = x^2 + y[/tex]

y(0) = 1

h = 0.01 (step size)

x = 0.02 (desired x-value)

The general formula for the second-order Runge-Kutta method is:

y(i+1) = y(i) + (k1 + k2)/2

where

k1 = h * f(x(i), y(i))

k2 = h * f(x(i) + h, y(i) + k1)

Let's calculate the values step by step:

Set x(0) = 0, y(0) = 1.

k1 = h * f(x(0), y(0))

[tex]= 0.01 * (0^2 + 1)[/tex]

  = 0.01

k2 = h * f(x(0) + h, y(0) + k1)

[tex]= 0.01 * ((0 + 0.01)^2 + 1 + 0.01)[/tex]

  = 0.01 * (0.0001 + 1.01)

  = 0.010101

y(1) = y(0) + (k1 + k2)/2

    = 1 + (0.01 + 0.010101)/2

    = 1 + 0.020101/2

    = 1.0100505

Let's perform the calculations iteratively:

Iteration 1:

x = 0.01

y = 1.0100505 (from Step 4)

Iteration 2:

Now we need to repeat steps 2-4 with the new x and y values:

k1 = h * f(x(1), y(1))

[tex]= 0.01 * (0.01^2 + 1.0100505)[/tex]

  = 0.0102010050025

k2 = h * f(x(1) + h, y(1) + k1)

[tex]= 0.01 * ((0.01 + 0.01)^2 + 1.0100505 + 0.0102010050025)[/tex]

  = 0.010307015102525

y(2) = y(1) + (k1 + k2)/2

    = 1.0100505 + (0.0102010050025 + 0.010307015102525)/2

    = 1.0203045100525125

After the second iteration, when x = 0.02,

we obtain y ≈ 1.0203045100525125.

Therefore, the approximate value of y when x = 0.02 using the Runge-Kutta method of second order is 1.0203045100525125.

Learn more about Runge-Kutta method

brainly.com/question/30267790

#SPJ11

the values of x and y that satisfy the given equation are x = 1 and y = -1.

To determine the values of x and y in the equation:

(4+2i)(x+yi) + (3-2i) = 9-4i

We can expand the left side of the equation using the distributive property:

(4x + 2ix + 4yi - 2y) + (3 - 2i) = 9 - 4i

Group the real and imaginary terms together:

(4x - 2y + 3) + (2ix + 4yi - 2i) = 9 - 4i

Now, equating the real parts and imaginary parts on both sides of the equation, we have:

Real Part:

4x - 2y + 3 = 9

Imaginary Part:

2ix + 4yi - 2i = -4i

From the real part equation, we can solve for x and y:

4x - 2y = 9 - 3

4x - 2y = 6

2x - y = 3      (Dividing by 2)

From the imaginary part equation, we can solve for x and y:

2ix + 4yi - 2i = -4i

2ix + 4yi = -4i + 2i

2ix + 4yi = -2i

2x + 4y = -2      (Dividing by i)

Now, we have a system of linear equations:

2x - y = 3

2x + 4y = -2

To solve this system, we can use the method of substitution or elimination. Let's use the elimination method:

Multiply the first equation by 2 to eliminate the x term:

(2)(2x - y) = (2)(3)

4x - 2y = 6

Now, subtract the second equation from the modified first equation:

(4x - 2y) - (2x + 4y) = 6 - (-2)

4x - 2x - 2y - 4y = 6 + 2

2x - 6y = 8

Simplifying further, we get:

2x - 6y = 8    ---(3)

Now, we have two equations:

2x + 4y = -2   ---(2)

2x - 6y = 8    ---(3)

Multiply equation (2) by 3 and equation (3) by 2 to eliminate the x term:

(3)(2x + 4y) = (3)(-2)

(2)(2x - 6y) = (2)(8)

6x + 12y = -6   ---(4)

4x - 12y = 16   ---(5)

Add equations (4) and (5) to eliminate the y term:

(6x + 12y) + (4x - 12y) = -6 + 16

10x = 10

x = 10/10

x = 1

Substitute the value of x back into equation (2):

2(1) + 4y = -2

2 + 4y = -2

4y = -2 - 2

4y = -4

y = -4/4

y = -1

To know more about equation visit:

brainly.com/question/29538993

#SPJ11

The measure of the arc angle JA is 76 degrees.

The sum of angles in a cyclic quadrilateral is 360 degrees. The opposite angles in a cyclic quadrilateral is supplementary.

The measure of an arc intercepted by an angle of a quadrilateral that is inscribed in a circle is equal to two times the measure of the inscribed angle.

Therefore,

26x + 1 = 1 / 2 (18x + 4 + 6 + 32x)

26x + 1 = 1 / 2 (50x + 10)

26x + 1 = 25x + 5

26x - 25x = 5 - 1

x = 4

Therefore,

arc angle JA = 18x + 4

arc angle JA = 18(4) + 4

arc angle JA =72 + 4

arc angle JA = 76 degrees.

learn more on arc angle here: brainly.com/question/30818451

#SPJ1

The area of the sidewalk is total area of the square and the two semicircles, and then subtract the area of the garden itself i.e 2.25 square meters.

To find the area of the sidewalk surrounding the garden, we need to calculate the total area of the square and the two semicircles, and then subtract the area of the garden itself.

Let's break down the steps to calculate the area of the sidewalk:

Area of the square:

The side length of the square is equal to the diameter of the semicircle, which is 2 * 10 = 20 meters.

The area of the square is given by the formula: side length * side length = 20 * 20 = 400 square meters.

Area of the two semicircles:

The radius of each semicircle is 10 meters, so the area of one semicircle is (1/2) * π * radius² = (1/2) * π * 10² = 50π square meters.

Since there are two semicircles, the total area of the semicircles is 2 * 50π = 100π square meters.

Area of the garden:

The area of the garden is the combined area of the square and the two semicircles, which is 400 + 100π square meters.

Area of the sidewalk:

The width of the sidewalk is 1.5 meters, and it surrounds the garden along its edge. To find the area of the sidewalk, we subtract the area of the garden from the area of the garden plus the sidewalk.

Area of the sidewalk = (400 + 100π) - (400 + 100π - 1.5 * 1.5) square meters.

Simplifying the equation, we have:

Area of the sidewalk = 1.5 * 1.5 square meters.

Therefore, the area of the sidewalk is 2.25 square meters.

Learn more about area here:

https://brainly.com/question/16151549

#SPJ11

The value of the integral is 1/(10a²).

The integral to be evaluated is:

∫₀^(10) a dx / (a² x²)^(3/2)

We can simplify the denominator as follows:

(a² x²)^(3/2) = a³ x³

So, the integral becomes:

∫₀^(10) a dx / a³ x³

= ∫₀^(10) dx / (a² x²)

= (1/a²) ∫₀^(10) dx / x²

= (1/a²) [-1/x]₀^(10)

= 1/(a² × 10)

= 1/(10a²)

Therefore, the value of the integral is 1/(10a²).

Learn more about integral here

https://brainly.com/question/30094386

#SPJ11

The best point estimate for the ratio of population variances can be calculated using the F-statistic:

F = s1^2 / s2^2

where s1^2 is the sample variance of the first population, and s2^2 is the sample variance of the second population.

Given the sample statistics:

n1 = 24

n2 = 23

s1^2 = 55.094

s2^2 = 30.271

The F-statistic can be calculated as:

F = s1^2 / s2^2 = 55.094 / 30.271 = 1.8187

The point estimate for the ratio of population variances is therefore 1.8187. Rounded to four decimal places, the answer is 1.8187.

To know more about ratio, refer here :

https://brainly.com/question/13419413#

#SPJ11

By mathematical induction, the equation 1 + 3 + 5 + ... + (2n - 1) = n² is true for every positive integer n.

Using mathematical induction, we can verify that the equation 1 + 3 + 5 + ... + (2n - 1) = n² is true for every positive integer n.
Base case (n=1): 2(1) - 1 = 1, and 1² = 1, so the equation holds for n=1.
Inductive step: Assume the equation is true for n=k, i.e., 1 + 3 + ... + (2k - 1) = k². We must prove it's true for n=k+1.
Consider the sum 1 + 3 + ... + (2k - 1) + (2(k+1) - 1). By the inductive hypothesis, the sum up to (2k - 1) is equal to k². Thus, the new sum is k² + (2k + 1).
Now, let's examine (k+1)²: (k+1)² = k² + 2k + 1.
Comparing the two expressions, we find that they are equal: k^2 + (2k + 1) = k² + 2k + 1. Therefore, the equation holds for n=k+1.
By mathematical induction, the equation 1 + 3 + 5 + ... + (2n - 1) = n² is true for every positive integer n.

Learn more about integer here:

https://brainly.com/question/1768254

#SPJ11

The slant height of the cone is approximately 6.37 inches.

To find the slant height of the cone, we can use the formula for the surface area of a cone, which is given by A = πr(r + l), where A is the surface area, r is the radius, and l is the slant height. We are given that the surface area is 16.8π square inches and the radius is 3 inches. Substituting these values into the formula, we get 16.8π = π(3)(3 + l).

To solve for l, we can simplify the equation: 16.8π = 9π + πl. By subtracting 9π from both sides, we get 7.8π = πl. Dividing both sides by π, we find that the slant height, l, is approximately 7.8 inches.

Therefore, the slant height of the cone is approximately 6.37 inches.

Learn more about height here:

https://brainly.com/question/32560368

#SPJ11

The sequence x² - 64 is not a geometic sequence

From the question, we have the following parameters that can be used in our computation:

x to the second power minus 64

Express properly

So, we have

x² - 64

The above expression is a quadratic expression

This is because it has a degree of 2 and a constant term

So, the sequence is not a geometic sequence

Read more about sequence at

https://brainly.com/question/30499691

#SPJ1

The volume of the composite figure of the cylinder and the cone is 485.65 cm³

Given a composite figure.

It consists of a cylinder and a cone.

Volume of cylinder = π r² h, where r is the radius and h is the height of the cylinder.

Here r = 4 cm and h = 7 cm

Volume of cylinder = π (4)² (7)

                                = 112π cm³

Volume of the cone = 1/3 π r² h, where r is the radius and h is the height of the cone.

Here r = 4 cm and h = 8 cm

Volume of cylinder = 1/3 π (4)² (8)

                                = 42.67π cm³

Total volume = 112π cm³ + 42.67π cm³

                      = 154.67π cm³

                      = 485.65 cm³

Hence the volume is 485.65 cm³.

Learn more about Volume here :

https://brainly.com/question/28058531

#SPJ1

Answer:

D

Step-by-step explanation:

It seems that you're asking about solving a system of differential equations using the elimination method. Unfortunately, the elimination method is used for solving systems of linear equations, not differential equations. The given system consists of second-order nonlinear differential equations.

To use the elimination method to solve the system:

1. Start by multiplying the first equation by y2 and the second equation by -y1.

2. This gives us:

y′′1y2 = 2y1y2t

-y′′2y1 = -y12y2et

3. Now we can add the two equations together:

y′′1y2 - y′′2y1 = 2y1y2t + y12y2et

4. This simplifies to:

(y1y2)'' = 2y1y2t + y12y2et

5. Finally, we can integrate both sides to get the solution:

y1y2 = ∫(2t + e-t) dt

y1y2 = t2 - e-t + C

where C is a constant of integration.

Therefore, the solution to the system using the elimination method is:

y1y2 = t2 - e-t + C

For such problems, you may want to consider using numerical methods like Euler's method or Runge-Kutta methods to obtain approximate solutions, or consult with a specialist in differential equations to explore other possible techniques for solving the given system.

To learn more about Elimination Method: brainly.com/question/13877817

#SPJ11

Main Answer:To solve this equation, we need an initial condition or boundary condition to determine the specific solution. Once we have the solution for z, we can substitute it back into the first equation (y′′ = 2yzt) to find the solution for y.

Supporting Question and Answer:

How do we solve a system of differential equations using the elimination method?

To solve a system of differential equations using the elimination method, we differentiate the equations and manipulate them to eliminate one variable at a time. This allows us to express one variable in terms of the other variables, reducing the system to a simpler set of equations.

Body of the Solution: To solve the system of differential equations using the elimination method, we will eliminate one variable at a time by differentiating the equations. Let's denote y₁ as y and y₂ as z for simplicity.

Given system:

y′′ = 2yzt z′′ = 2yz - e^t

Step 1: Differentiate the first equation with respect to t. y′′′ = 2(z′t + z) + 2yzt

Step 2: Substitute the value of y′′′ into the second equation. 2(z′t + z) + 2yzt = 2yz - e^t

Simplifying the equation:

2z′t + 2z + 2yzt = 2yz - e^t

Step 3: Rearrange the terms to isolate z′.

2z′t + 2z - 2yz + e^t = 0

Step 4: Divide the equation by 2t to isolate z′.

z′ + z/t - y + e^t/2t = 0

This equation represents a first-order linear differential equation in terms of z.

Final Answer:The single required equation is: z′ + z/t - y + e^t/2t = 0

To learn more about a system of differential equations using the elimination method from the given link

https://brainly.com/question/25427192

#SPJ4

The solution to the initial value problem is y=x-x^2-xln(x)(ln(x)-1)+(x/2)(ln(x))^2.

To find Green's function for the given differential equation, we first need to solve the homogeneous equation:

x^2y''-2xy'+2y=0

This is a Cauchy-Euler equation, so we try a solution of the form y=x^r. Substituting this into the equation, we get:

r(r-1)x^r-2rx^r+2x^r=0

Simplifying, we get:

r(r-1)=0

which gives us r=0 or r=1. Therefore, the general solution to the homogeneous equation is:

y_h=c_1x+c_2x^2

Next, we find a particular solution to the non-homogeneous equation using a variety of parameters. We assume that the particular solution has the form y_p=u(x)y_1+v(x)y_2, where y_1 and y_2 are linearly independent solutions to the homogeneous equation. We can take y_1=x and y_2=x^2. Then,

y_1'=1, y_2'=2x, y_1''=0, y_2''=2

Substituting these into the differential equation, we get:

x^2(u''(x)x+v''(x)x^2)+(2x(u'(x)x+v'(x)x^2))+(2(u(x)x+v(x)x^2))=xln(x)

Simplifying, we get:

x^2u''(x)+2xu'(x)-xv'(x)+2u(x)=xln(x)

x^3v''(x)-2x^2v'(x)+2xv(x)=0

We can solve the second equation using the same method as before, and find the two linearly independent solutions:

y_1=x, y_2=xln(x)

Then, we can solve for u(x) and v(x) using the formula:

u(x)=-∫(y_2(x)f(x))/(W(y_1,y_2)(x))dx + C_1

v(x)=∫(y_1(x)f(x))/(W(y_1,y_2)(x))dx + C_2

where W(y_1,y_2)(x) is the Wronskian of y_1 and y_2.

Evaluating these integrals, we get:

u(x)=-∫(xln(x)ln(x))/(x)dx + C_1 = -xln(x)(ln(x)-1)+C_1

v(x)=∫(xln(x)dx)/(x) + C_2 = (x/2)(ln(x))^2+C_2

Therefore, the particular solution is:

y_p=-xln(x)(ln(x)-1)+(x/2)(ln(x))^2

Finally, the general solution to the non-homogeneous equation is:

y=y_h+y_p=c_1x+c_2x^2-xln(x)(ln(x)-1)+(x/2)(ln(x))^2

Using the initial conditions y(1)=1 and y'(1)=0, we can solve for the constants c_1 and c_2:

c_1=1, c_2=-1/2

Therefore, the solution to the initial value problem is:

y=x-x^2-xln(x)(ln(x)-1)+(x/2)(ln(x))^2

Learn more about Green's function

brainly.com/question/7970636

#SPJ11